위상수학이란 무엇인가 – 도넛과 커피잔의 수학적 관계

위상수학(Topology)은 도형의 모양이 아니라 연속적인 성질에 주목하는 수학 분야로, 도형을 자르거나 붙이지 않고 ‘늘이고 줄이는’ 방식으로 탐구한다. 대표적인 예시로 자주 언급되는 것이 도넛과 커피잔이다. 겉보기엔 전혀 다르게 생긴 두 물체지만, 수학적으로는 구멍이 하나라는 동일한 위상적 성질을 공유하기 때문에 동일한 구조로 분류된다. 본문에서는 이러한 위상동치의 개념, 연속성과 변형, 수학적으로 위상이 어떻게 분류되는지, 현대 과학에서의 활용까지 폭넓게 살펴본다.

위상수학의 정의와 개념

위상수학이란?

위상수학(Topology)은 전통적인 기하학과는 다른 방식으로 도형과 공간을 연구하는 수학 분야다. 위상수학의 핵심은 도형의 '모양'이 아니라, '형태의 본질적인 구조'에 주목하는 것이다. 예를 들어, 삼각형과 정사각형은 서로 다른 도형처럼 보이지만, 위상수학적 관점에서는 이 둘 모두 ‘연속적인 변형’을 통해 서로 전환될 수 있기 때문에 같은 구조로 본다.

여기서 말하는 '연속적인 변형'이란 자르거나 찢지 않고, 늘리거나 구부리는 방식으로 형태를 바꾸는 과정을 의미한다. 즉, 고무밴드처럼 유연하게 변형이 가능하다면 그것은 위상적으로 동등한 것으로 간주된다.

기하학과 위상수학의 차이점

기하학에서는 길이, 각도, 면적, 부피 등이 중요한 측정 기준이다. 그러나 위상수학은 그런 양적인 정보보다 '연속성', '연결성', '구멍의 개수'와 같은 성질에 집중한다. 기하학에서의 정밀한 도형 분석이 엔지니어링과 설계에 유용하다면, 위상수학은 복잡한 데이터 구조, 물리학의 시공간 이론, 컴퓨터 그래픽스 등 추상적인 구조 해석에 적합하다.

 

위상적 성질이란 무엇인가?

위상적 성질은 도형을 아무리 변형해도 변하지 않는 속성이다. 가장 대표적인 위상적 성질은 다음과 같다:

• 연결성(Connectedness): 도형이 하나로 이어져 있는가?
• 구멍의 개수: 도형에 뚫려 있는 빈 공간의 수는 몇 개인가?
• 경계의 유무: 도형이 닫혀 있는가, 열린 형태인가?

이러한 위상적 성질은 연속 함수와 위상 공간의 개념을 바탕으로 수학적으로 정의되고 분석된다.

---

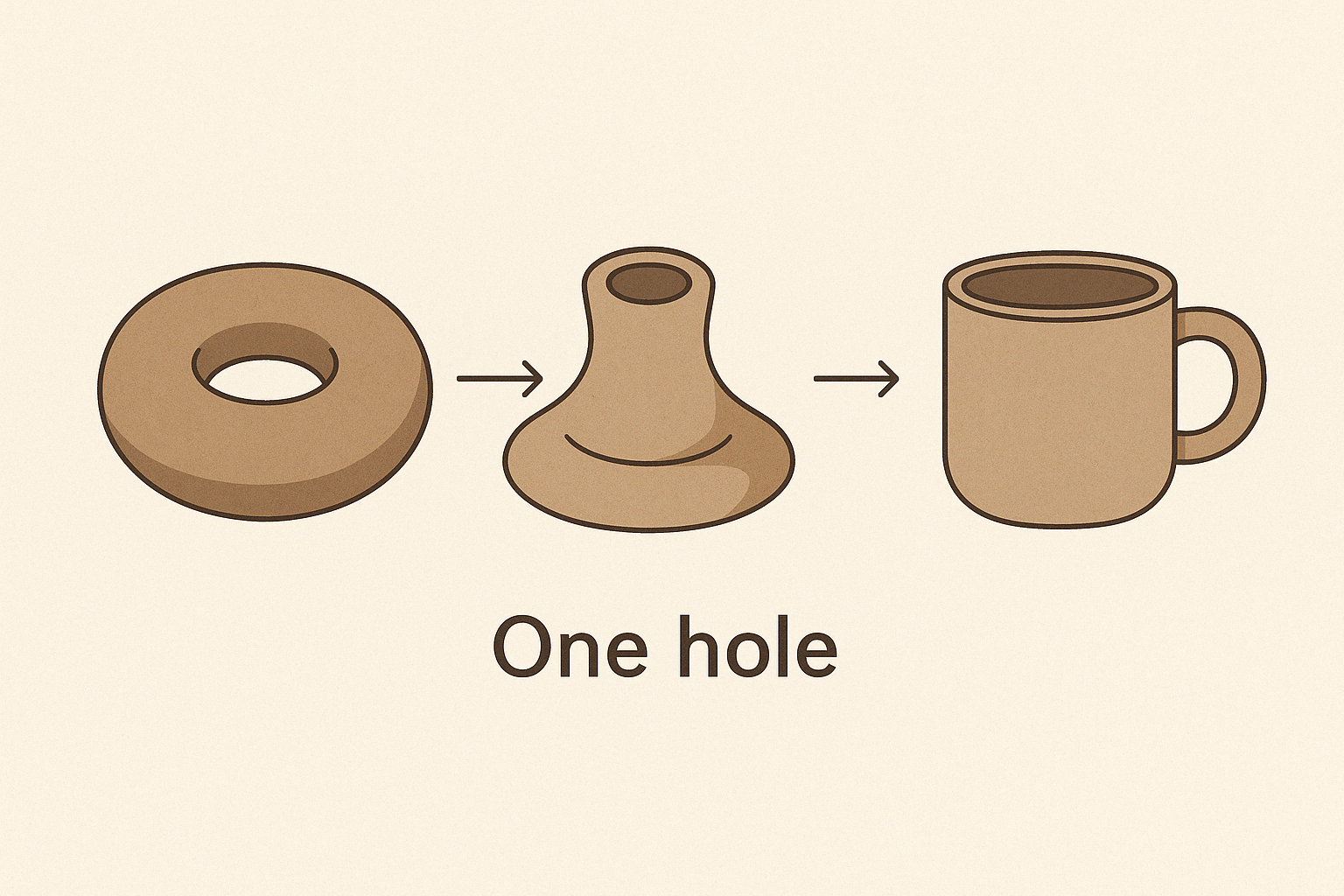
위상수학이란 무엇인가 – 도넛과 커피잔의 수학적 관계

도넛과 커피잔 – 위상동치의 대표 사례

도넛과 커피잔은 왜 같은가?

위상수학에서 자주 언급되는 대표적인 예시가 바로 "도넛(donut)"과 "커피잔(coffee mug)"이다. 일반적으로 보면 두 사물은 형태가 매우 다르다. 도넛은 둥글고 구멍이 중앙에 있으며, 커피잔은 컵 모양에 손잡이가 달려 있다. 하지만 위상수학적으로는 이 둘은 서로 위상적으로 동등, 즉 *위상동치(Topological equivalence)*다.

이유는 간단하다. 두 도형 모두 구멍이 하나라는 구조적 특징을 공유하고 있기 때문이다. 도넛의 중앙 구멍과 커피잔 손잡이의 구멍은 본질적으로 동일한 위상적 구조로 취급된다.

구멍의 개수와 연속적 변형

위상수학에서 중요한 개념 중 하나는 'genus(지니수)'다. 이는 도형에 있는 구멍의 수를 정수로 표현한 값이다. 도넛과 커피잔은 지니수 1(genus = 1)을 가지며, 이는 이들이 찢지 않고도 서로 변형될 수 있음을 수학적으로 보장한다. 도넛의 몸통을 잡아당기면 손잡이가 형성되고, 중심 부분을 오목하게 눌러 컵처럼 만들 수 있다. 이렇게 형상을 부드럽게 바꾸는 과정을 통해 도넛 → 커피잔으로 전환이 가능하다.

위상동형(Homeomorphism)의 의미

위상수학에서 "위상동형(homeomorphism)"이란 두 위상공간이 연속적인 함수로 서로 대응되며, 그 역함수도 연속적인 관계를 의미한다. 쉽게 말하면, 자르지 않고 이어붙이지 않고 도형을 유연하게 변형해서 같은 구조가 되는 것이다. 도넛과 커피잔은 위상동형의 대표적인 예다.

이 개념은 공학, 생물학, 데이터 해석 등 다양한 분야에서 복잡한 구조의 동등성을 판별하는 데 매우 유용하게 쓰인다.

---

위상수학의 핵심 개념들

연속성의 수학적 정의

위상수학은 '연속적 변형'을 다루는 수학이므로, "연속성(continuity)"의 개념이 매우 중요하다. 고등학교 수학에서 배운 함수의 연속성은 위상수학에서 확장되어 사용된다.

공식적으로는, 함수 f: X → Y가 연속이라 함은 X의 열린 집합의 원상이 Y에서도 열린 집합이 되는 조건을 만족하는 경우를 말한다. 이는 매우 일반적이고 강력한 개념으로, 모든 함수적 분석의 기반이 된다.

위상공간과 열린집합

모든 위상수학은 위상공간(topological space) 위에서 정의된다. 이는 다음의 두 요소로 구성된다:

• 집합 X: 우리가 연구하려는 도형이나 공간
• 위상 T: X에서 ‘열린 집합’이라 부를 수 있는 부분집합들의 모임

이러한 구조 위에서 연속성, 경계, 폐집합, 콤팩트성, 연결성 등이 정의된다. 간단히 말해, 위상공간은 공간 내의 구조적 특성을 수학적으로 분석 가능한 상태로 만든 프레임이라고 볼 수 있다.

연결성, 콤팩트성 등 주요 성질

• 연결성(Connectedness): 한 덩어리로 연결된 공간인가?
• 콤팩트성(Compactness): 유한한 열린 집합으로 덮을 수 있는가?
• 경계(Boundary): 공간의 가장자리가 존재하는가?

이러한 성질은 복잡한 수학적 구조나 데이터 세트가 어떤 성격을 가지는지 파악하는 데 사용된다.

---

위상수학의 실제 응용 사례

데이터 과학과 위상수학 (TDA)

"TDA(Topological Data Analysis)"는 빅데이터의 구조적 특징을 위상수학으로 해석하는 신흥 분야다. 고차원 데이터의 군집, 패턴, 형태를 파악할 수 있어 의료 데이터 분석, 유전자 데이터 해석, 금융 시장 분석 등에 널리 사용된다.

예를 들어, 수백 개의 유전자 표현 데이터를 위상수학적 거리로 재구성하면 암 환자와 비환자 그룹을 나누는 구조적 차이를 시각화할 수 있다.

물리학에서의 위상적 위상수학 (예: 양자 홀 효과)

물리학에서 위상수학은 양자역학과 응집물질물리학의 핵심 도구로 쓰인다. 특히 양자 홀 효과, 위상절연체(topological insulator), 양자장론에서는 도형의 위상적 성질이 전자의 상태, 스핀, 흐름과 깊이 관련된다.

예를 들어, 특정 전자 상태는 도형의 '구멍' 개수와 관련이 있으며, 위상수가 바뀌지 않기 때문에 외부 자극에도 안정적인 물리 현상이 유지된다.

예술, 그래픽, 생물학 속 위상 응용

• 컴퓨터 그래픽스: 3D 모델링에서 메시(mesh)의 연속성과 변형을 위상수학적으로 처리
• 생물학: 단백질의 구조 해석에서 구멍의 개수와 연결성 분석
• 예술: 모빌, 종이접기, 나선형 조각 등에서 위상적 형태감 강조

---

형태 너머의 본질을 찾는 수학

수학적 사고 확장의 출발점

위상수학은 단순히 복잡한 개념의 수학이 아니라, 현실 속 숨겨진 구조를 드러내는 도구다. 도넛과 커피잔처럼 보이는 구조 속에서 진짜 본질은 ‘구멍 하나’라는 구조적 정보라는 점은 우리에게 큰 통찰을 준다.

이는 "보이는 것 너머를 보는 힘", 즉 수학적 사고력의 핵심이다.

위상수학이 던지는 철학적 질문

마지막으로 위상수학은 우리에게 중요한 질문을 던진다.

• 형태는 본질을 담는가?
• 서로 다른 것은 진짜 다른가?
• 수학은 현실의 진실을 어떻게 드러내는가?

이러한 질문을 통해 우리는 수학을 단순 계산이 아니라, 철학적이고 창의적인 사고의 도구로 받아들이게 된다.