최적화 이론 – 실생활에 숨겨진 라그랑지 승수의 원리

최적화는 우리가 자원을 최대한 효율적으로 사용하고자 할 때 반드시 알아야 할 수학 개념이다. 특히 제한 조건이 주어진 상황에서 최적의 해를 구하는 방법으로는 라그랑지 승수법이 널리 활용된다. 이 글에서는 라그랑지 승수의 기본 원리부터 이를 실생활 문제와 경제 모델에 어떻게 적용할 수 있는지를 자세히 설명한다. 제한된 예산으로 최대 효과를 내는 마케팅 전략, 생산 효율을 극대화하는 기업의 의사결정 등 다양한 예시를 통해 이론을 쉽게 풀어낸다. 수학적 개념에 익숙하지 않은 사람들도 이해할 수 있도록 도식과 함께 단계별로 정리하며, 고등수학과 경제학, 공학 문제에 실제로 활용되는 방식까지 폭넓게 소개할 예정이다.

최적화 이론 – 실생활에 숨겨진 라그랑지 승수의 원리

최적화 이론 – 실생활에 숨겨진 라그랑지 승수의 원리

라그랑지 승수란 무엇인가? – 제한 조건 최적화의 핵심

우리는 일상에서 다양한 최적화 문제를 마주친다. 제한된 자원으로 최고의 효율을 내는 것이 그 예다. 예를 들어, 한정된 예산으로 최대한의 광고 효과를 내거나, 일정한 시간 내에 학습 효율을 극대화하는 것이다. 이러한 문제는 수학적으로 "제약 조건이 있는 최적화 문제"로 정의된다.

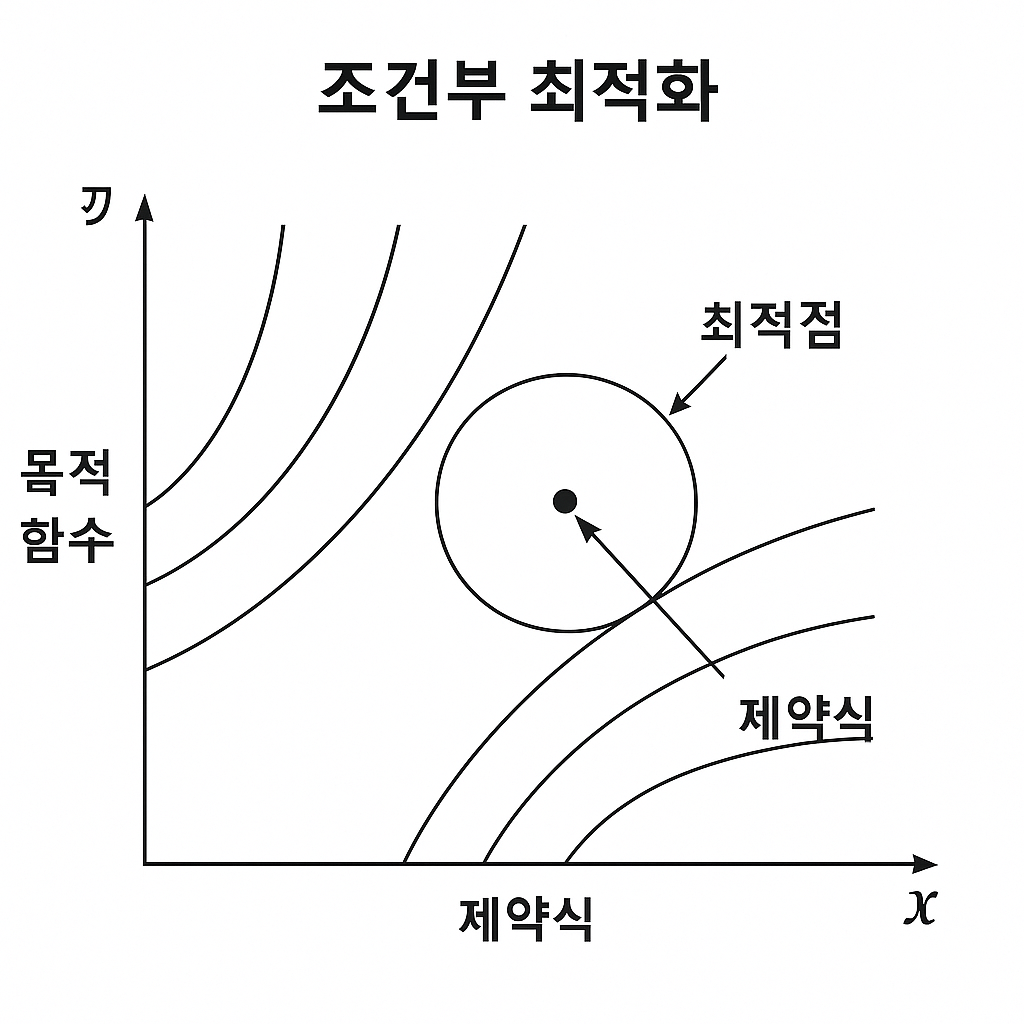
라그랑지 승수법은 이러한 제한 조건이 있는 최적화 문제를 푸는 강력한 도구다. 특정 함수의 극값을 구할 때, 제한 조건을 만족하는 조건 하에서 해를 찾기 위해 사용된다. 이를 위해 "라그랑지 함수(Lagrangian function)"라는 새로운 함수를 정의한다:

L(x, y, λ) = f(x, y) - λ(g(x, y) - c)

여기서 f(x, y)는 목적 함수, g(x, y) = c는 제한 조건, λ는 라그랑지 승수다.

---

라그랑지 승수의 원리 – 미분을 활용한 접근

최적화의 핵심은 함수의 극값을 찾는 것이다. 라그랑지 함수의 각 변수에 대해 편미분하고 이를 0으로 두면 최적해를 구할 수 있다.

예시 문제:

maximize f(x, y) = x + y
subject to x² + y² = 1

라그랑지 함수는 다음과 같다:

L(x, y, λ) = x + y - λ(x² + y² - 1)

각 변수에 대해 편미분한 뒤 식을 세운다:

∂L/∂x = 1 - 2λx = 0
∂L/∂y = 1 - 2λy = 0
∂L/∂λ = -(x² + y² - 1) = 0

이 식들을 연립하여 풀면 최적의 x, y 값을 구할 수 있다. 이 방식은 제한 조건과 목적 함수의 기울기가 동일한 방향을 가리키는 지점을 찾는 과정이다.

---

 

실생활 속 라그랑지 승수 활용 사례 – 조건 최적화의 현실 응용

라그랑지 승수법은 단지 이론에 그치지 않는다. 우리의 일상 속에서도 다양한 방식으로 적용된다.

1: 마케팅 전략 최적화

기업이 광고 예산 1억 원을 A, B, C 채널에 배분해 최대 노출 효과를 얻고 싶다고 해보자. 각 채널의 노출 기여도가 다르고, 총액 1억을 넘지 않아야 한다면 이건 명백한 제약 조건 문제다. 라그랑지 승수를 이용하면 최적 분배 전략을 도출할 수 있다.

2: 식단 조절

건강을 위해 하루 2,000kcal를 넘지 않으면서 단백질 섭취를 극대화하고 싶은 사람도 있다. 이때 각 식품의 열량과 단백질 수치를 함수로 구성하고 라그랑지 승수를 활용하면 이상적인 식단 조합을 수학적으로 구할 수 있다.

 3: 시간 관리

하루 24시간 안에 공부, 운동, 휴식의 효율적 비율을 찾고 싶은 경우도 마찬가지다. 시간은 제한되어 있고, 각 활동의 만족도를 수식으로 나타내 최적화하는 방식으로 적용할 수 있다.

 

경제 수학에서의 활용 – 소비자와 생산자의 최적화 문제

• 소비자 최적화: 소비자가 예산 내에서 효용을 최대화하려고 할 때, 효용 함수와 예산 제약 조건을 결합해 최적 소비 조합을 구할 수 있다.
• 예: U(x, y)를 최대화, subject to px + qy = M
• 생산자 최적화: 기업이 제한된 자본과 노동으로 최대 생산량을 달성하고자 할 때, 생산 함수와 비용 제한 조건을 통해 최적 투입 조합을 산출한다.
• 예: Q(K, L) 최대화, subject to wK + rL = C

• 경제학에서도 라그랑지 승수는 핵심 개념이다.

---

최적화 이론 – 실생활에 숨겨진 라그랑지 승수의 원리

라그랑지 승수의 확장 개념 – KKT 조건과 현대 최적화 이론

라그랑지 승수는 등식 제약 조건만 다루지만, 현실에서는 부등식 제약 조건도 많다. 예를 들어, ‘예산은 최대 1억까지’라는 조건은 부등식이다.

이를 해결하기 위해 KKT(Karush-Kuhn-Tucker) 조건이 도입된다. 이는 라그랑지 승수를 확장하여, 불평등 제약과 비선형 목적 함수도 다룰 수 있게 한다.

 

 KKT 조건 간단 요약

1. 목적 함수 및 제약 조건이 미분 가능해야 함
2. 라그랑지 함수에 부등식 제약 포함
3. 최적해는 정해진 조건(Complementary Slackness 등)을 만족해야 함

이러한 조건들은 AI 최적화, 머신러닝, 투자모델, 공급망 설계 등 현대 산업 전반에서 필수적인 수단으로 작용한다.

실제 문제에서는 등식 제약뿐 아니라 불평등 제약도 등장한다. 예를 들어 “비용은 100만 원 이하여야 한다”는 조건은 불평등 제약이다.

이럴 경우 라그랑지 승수만으로는 부족하고, 확장된 기법인 "KKT 조건(Karush-Kuhn-Tucker conditions)"을 사용한다. 이는 현대 최적화 이론에서 중요한 도구로, 머신러닝, 경제학, 물류 계획 등 다양한 분야에 응용된다.

---

 

나의 생각

라그랑지 승수는 제한 조건이 있는 상황에서 최적해를 구하는 수학적 방법으로, 경제학, 공학, 경영학 등 다양한 분야에 응용된다. 실생활에서도 그 원리를 이해하면 의사결정의 질이 높아지고, 보다 효율적인 선택을 할 수 있게 된다. 복잡해 보이지만, 한 번 원리를 이해하면 무궁무진한 활용이 가능한 강력한 도구다.